学习笔记
跟着卡哥学算法Day 16：二叉树常见题目4
正在加载今日诗词....
2025-02-26

110.平衡二叉树 🌟🌟

力扣链接 🌟🌟

题目描述

给定一个二叉树，在q树的最后一行找到最左边的值。

示例 1:

给定二叉树 [2, 1, 3]

//       2
//      / \
//     1  3

输出：1

示例 2:

给定二叉树 [1, 2, 3, 4, 5, 6, 7]

//       1
//      / \
//     2  3
//    /  / \
//   4  5  6
//      /
//     7

输出：7

解题思路

  • 关键：在树的最底层找到最左边的值
  • 最底层：二叉树最大深度的一层
  • 最左边：该层中最靠左边的节点

递归

递归三部曲：

  1. 明确递归函数的参数和返回值

    • 参数 1：当前传入节点
    • 参数 2：当前节点的深度
    • 返回值：无

  2. 明确终止条件

    • 遇到叶子节点 !root.left && !root.right，当前深度与最大深度比较，大于最大深度，则更新最大深度 maxDepth 和最大深度最左边的值 result

  3. 确定单层递归逻辑

    • 分别计算左子树和右子树最大深度
function findBottomLeftValue(root) {
  let result = 0
  let maxDepth = 0

  const traverse = (node, depth) => {
    if (!node) return

    if (!node.left && !node.right) {
      if (depth > maxDepth) {
        maxDepth = depth
        result = node.val
      }
    }

    traverse(node.left, depth + 1)
    traverse(node.right, depth + 1)
  }

  traverse(root, 0)
}

迭代

求最后一行第一个节点的数值

function findBottomLeftValue(root) {
  if (!root) return null
  let result = 0
  const queue = [root]

  while (queue.length) {
    const length = queue.length
    for (let i = 0; i < length; i++) {
      const cur = queue.shift()
      if (i === 0) result = cur.val
      cur.left && queue.push(cur.left)
      cur.right && queue.push(cur.right)
    }
  }

  return result
}

112. 路径总和 🌟

力扣链接 🌟

题目描述

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

//       5
//      / \
//     4  8
//    /  / \
//   11 13 4
//   /\     \
//  7 2     1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

解题思路

递归

递归三部曲：

  1. 确定递归函数的参数和返回值

    • 参数 1：根节点
    • 参数 2：计数器，用来计算二叉树的一条边之和是否等于目标值
    • 返回值：bool

  2. 确定终止条件

    从根节点开始目标值递减，直到叶子节点时判断是否为 0

    if (!node.left && !node.right) {
  return count === 0
}

  3. 确定单层递归逻辑

    • 递归左右子节点，传递剩余和 count - cur.left.val count - cur.right.val
function hasPathSum(root, count) {
  if (!root) return false

  if (!root.left && !root.right) {
    return count === root.val
  }

  return (
    hasPathSum(root.left, count - root.val) ||
    hasPathSum(root.right, count - root.val)
  )
}

迭代

与递归不同，迭代记录当前路径和，再与目标值进行比较

步骤：

  1. 初始化栈：根节点和初始和存入栈
  2. 遍历栈：弹出节点及当前和，若为叶子且和等于目标值，返回 true
  3. 压入子节点：将左右子节点及更新后的和压入栈
function hasPathSum(root, count) {
  if (!root) return false

  const stack = [[root, root.val]]
  while (stack.length) {
    const [node, currentCount] = stack.pop()

    if (!node.left && !node.right && count === currentCount) {
      return true
    }

    node.left && stack.push([node.left, currentCount + node.left.val])
    node.right && stack.push([node.right, currentCount + node.right.val])
  }

  return false
}

113. 路径总和 II 🌟🌟

力扣链接 🌟🌟

题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

//       5
//      / \
//     4  8
//    /  / \
//   11 13 4
//   /\   / \
//  7 2   5 1

输出：[[5,4,11,2],[5,8,4,5]]

解题思路

递归

递归三部曲：

  1. 确定递归函数的参数和返回值

    • 参数 1：根节点
    • 参数 2：计数器，用来计算二叉树的一条边之和是否等于目标值
    • 返回值：void

  2. 确定终止条件

    从根节点开始目标值递减，当前节点是叶子节点且剩余和等于节点值 → 保存路径。

    if (!node.left && !node.right && node.val === count) {
}

  3. 确定单层递归逻辑

    • 递归左右子节点，传递剩余和 count - cur.val count - cur.val
    • 递归结束后回溯（从路径中移除当前节点）
function pathSum(root, count) {
  if (!root) return
  const result = []
  const currentPath = []

  const traverse = (node, targetNum) => {
    if (!node) return

    currentPath.push(node.val)
    if (!node.left && !node.right && node.val === targetNum) {
      result.push([...currentPath]) // 深拷贝 避免后续影响
    }

    node.left && traverse(node.left, targetNum - node.left.val)
    node.right && traverse(node.right, targetNum - node.right.val)
    currentPath.pop() // 回溯：移除当前节点
  }

  traverse(root, count)

  return result
}

迭代

用栈存储节点、剩余和及当前路径。遍历时更新路径和剩余和，遇到叶子节点且满足条件则保存路径。

步骤：

  1. 初始化栈：根节点、目标和、空路径入栈
  2. 遍历栈：弹出节点，若为叶子且剩余和等于节点值，保存路径
  3. 压入子节点：将左右子节点、更新后的剩余和及新路径压入栈
function pathSum(root, targetSum) {
  if (!root) return []

  const result = []
  const stack = [[root, targetSum, []]]
  while (stack.length) {
    const [node, currentCount, path] = stack.pop()

    const currentPath = [...path, node.val]
    if (!node.left && !node.right && node.val === currentCount) {
      result.push(currentPath)
    }

    node.left && stack.push([node.left, currentCount - node.val, currentPath])
    node.right && stack.push([node.right, currentCount - node.val, currentPath])
  }

  return result
}

106. 从中序与后序遍历序列构造二叉树 🌟🌟

力扣链接 🌟🌟

题目描述

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

//       3
//      / \
//     9  20
//       / \
//      15 7

解题思路

构造二叉树流程：

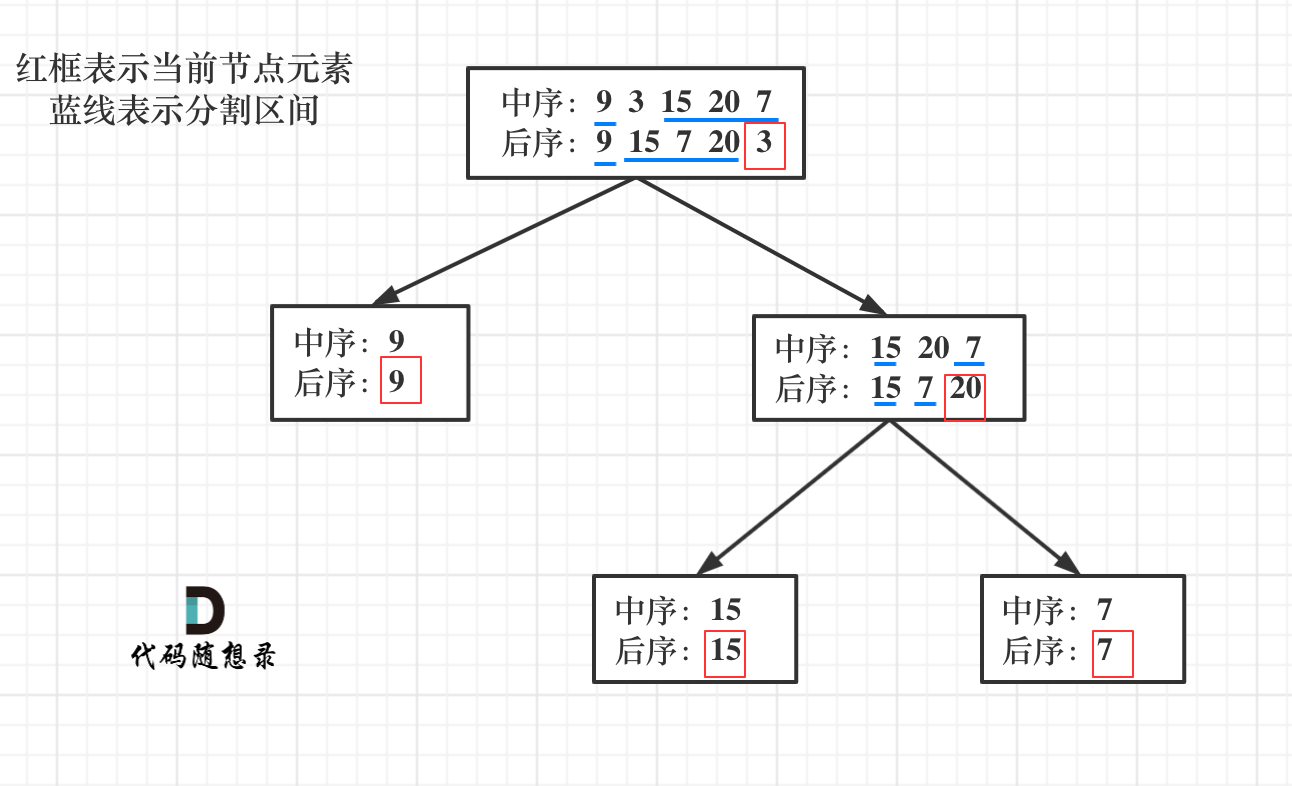
binary-tree-node

  1. 如果后序数组大小为零，说明时空节点，停止
  2. 如果不为空，取后序数组最后一个元素就是根节点（后序确定根节点）
  3. 找到后序数组最后一个元素在中序数组中的位置，作为切割点（中序分割左右子树）
  4. 切割中序数组，中序左数组作为左子树，中序右数组作为右子树
  5. 根据中序左数组长度
  6. 切割后序数组，切成后序左数组作为左子树，和后序右数组作为右子树
  7. 递归 1 - 5 步骤

递归三部曲

  1. 确定递归函数的参数和返回值

    • 参数 1：中序数组
    • 参数 2：后序数组
    • 返回值：根节点

  2. 确定终止条件

    • 数组长度为空时，返回 null

  3. 确定单层递归逻辑

    • 获取后序数组最后一个元素，作为根节点 const rootVal = postorder.pop()
    • 获取中序数组中根节点的 index const rootIndex = inorder.indexOf(rootVal)
    • 以根节点创建树 const root = new TreeNode(rootVal)
    • 递归构造左子树 root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex))
    • 递归构造右子树 root.right = buildTree(inorder.slice(rootIndex + 1), postorder.slice(rootIndex))

代码

function buildTree(inorder, postorder) {
  if (inorder.length === 0) return null

  const rootVal = postorder.pop()
  const rootIndex = inorder.indexOf(rootVal)
  const root = new TreeNode(rootVal)

  root.left = buildTree(
    inorder.slice(0, rootIndex),
    postorder.slice(0, rootIndex)
  )
  root.right = buildTree(
    inorder.slice(rootIndex + 1),
    postorder.slice(rootIndex)
  )

  return root
}

105. 从前序与中序遍历序列构造二叉树 🌟🌟

力扣链接 🌟🌟

题目描述

给给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

解题思路

代码

var buildTree = function (preorder, inorder) {
  if (!preorder.length) return null
  const rootVal = preorder.shift()
  const rootIndex = inorder.indexOf(rootVal)
  const root = new TreeNode(rootVal)

  root.left = buildTree(
    preorder.slice(0, rootIndex),
    inorder.slice(0, rootIndex)
  )
  root.right = buildTree(
    preorder.slice(rootIndex),
    inorder.slice(rootIndex + 1)
  )
  return root
}

京ICP备2022027737号
Copyright © 2022 - present @wangxiang

  • ☀️
  • 🌑